Matemática - 1º Bimestre
Formas geométricas e ângulos
01/02/2021
Formas geométricas
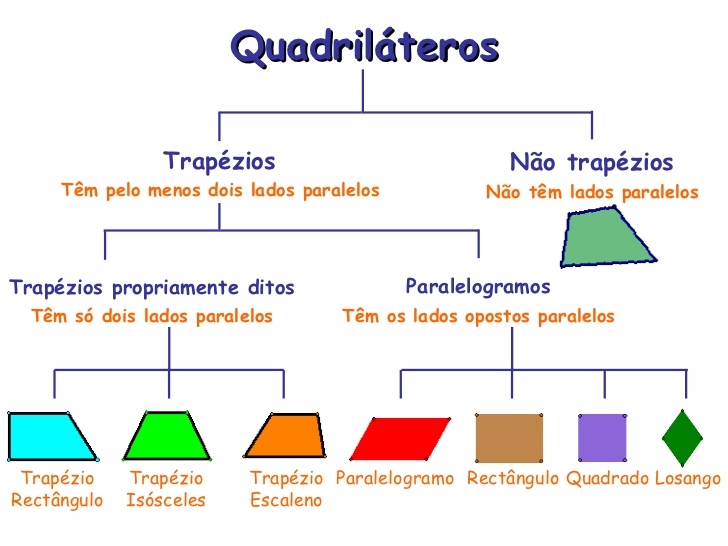
| Nome | Definição |
|---|---|
| Quadrilátero | Polígono de quadro lados |
| Trapésio | Pelo menos dois lados paralelos |
| Paralelogramos | Quatro lados paralelos (pares de lados paralelos) |
| Losango | Medidas iguais e paralelas sem ângulos retos ? |
| Retângulo | Todos os quatro lados paralelos e com angulos retos |
| Quadrado | Retângulo com lados iguais |
Ângulos
| Nome | Definição |
|---|---|
| Complementar | Ângulos em que a soma é 90° (ângulo reto) |
| Sumplementar | Que somam 180° (ângulo raso) |
| Oposto pelo vértice (OPV) | Auto-descritivo, estam opostos entre si pelo vértice |
| Alternos internos | localizados na região externa das retas paralelas |
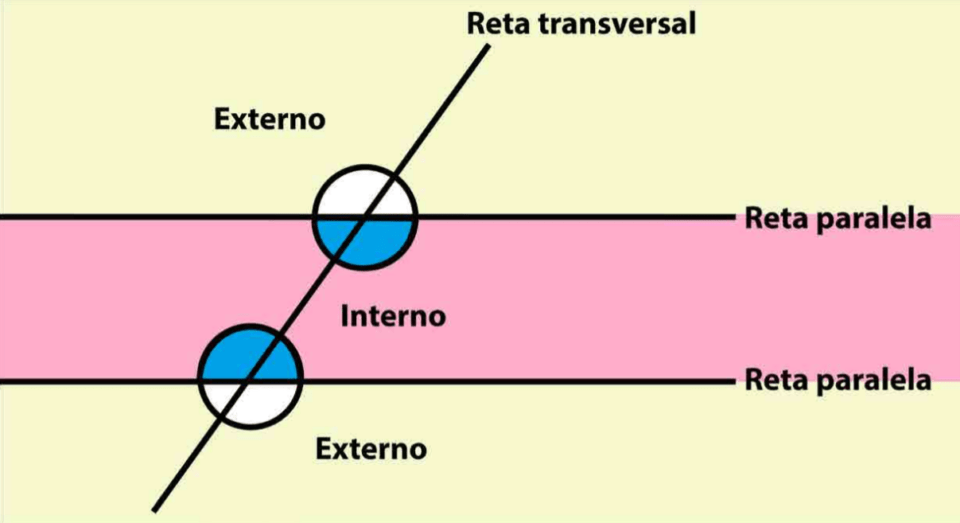
Exemplo alterno externo
Triângulos e ângulos internos
20/03/2021 — Aula 1
Foram revistos os conceitos de OPV e Alternos internos. (Comentamos sobre o Zorro :V)

Soma dos Ângulos Internos de um Triângulo
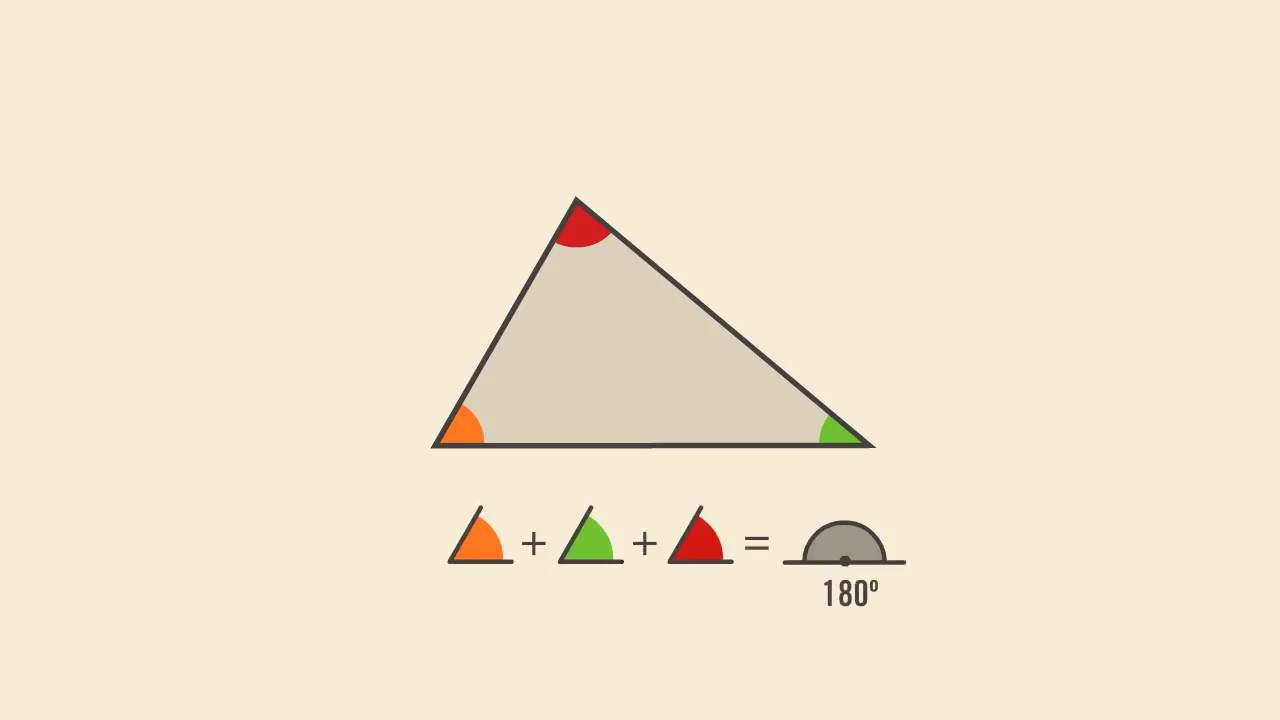
Demonstrações de exercícios
-
Foi feita uma demonstração de exercício, dados dois ângulos internos (30° e 80°), foi calculado o terceiro.
Sabendo que: 30° + 80° + x = 180° Temos que: x = 180° - (30° + 80°) Logo: x = 180° - 110° Finalmente: x = 70° - Num triângulo dentro de um retângulo, foram calculadas os valores dedos seus ângulos internos.
- Com dois triângulos (um em cima do outro) unidos pelo vértice, tínhamos que o ângulo interno do vértice do triângulo inferior valia 70°, logo, se aferiu o mesmo valor ao ângulo interno do vértice do triângulo superior.
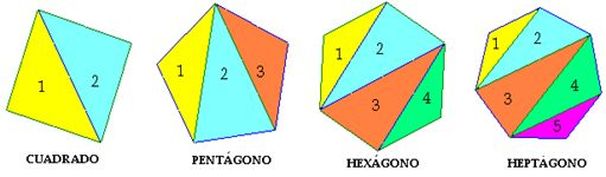
Ângulos internos de um polígono regular
Foi comentado que estudamos muito triângulos, pois, quando temos polígonos (regulares) mais complexos, podemos transformá-los em triângulos para facilitar a sua análise.
Porcentagem
02/03/2021 — Aula 2
Como discutimos, “porcentagem” ou “percentagem” estão corretos.
Porcentagem é considerar que algo é 100 (quando inteiro), para analisá-lo (em partes).
Muito ou pouco é relativo à o que é analisado.
Diferentes formas de calcular
Exemplo: 50% de R$ 16
Multiplicação
- Transformar a porcentagem para um decimal.
- No caso, 50% em 0,50 (30% seria 0,30 e 100% seria 1,00)
- Pegar o valor analisado e multiplicar.
- No caso, 16 * 0,50 = 8
Regra de três
100 - está para -> 16
assim como
50 -- está para -> x
100x = 16 * 50
100x = 800
x = 800 / 100
x = 8
Fácil
Proporção
Se 50 é a metade de 100, o resultado que procuramos é a metade de 16, logo 8.
Quando pensamos em proporção, devemos pensar em multiplicação e divisão, nunca adição.
Suponhamos que uma receita tem 1 lata de leite e 3 colheres de chocolate, se aumentarmos 1 lata, não devemos aumentar 1 colher (adicionando). Como multiplicamos a quantidade de latas por 2, devemos fazer o mesmo com as colheres, multiplicando 3 por 2, temos 6 colheres de chocolate.
Exercícios de porcentagem
04/03/2021
Revisamos o conceito de porcentagem e resolvemos 3 questões do Enem.
Dica: no Enem, sempre leia o final das questões antes do resto do enunciado.
Exercícios:
1 - O quadro representa os gastos mensais de uma família com internet, mensalidade escolar e mesada do filho.
| Internet | Mensalidade | Mesada |
|---|---|---|
| 120 | 700 | 400 |
No início do ano, a internet e a mensalidade escolar tiveram acréscimos, respectivamente, de 20% e de 10%. Necessitando manter o valor total da despesa mensal, a família reduzirá a mesada do filho. Qual será a porcentagem de redução da mesada?
a) 15,0
b) 23,5 <–
c) 30,0
d) 70,0
e) 76,5
Valor subtraído da internet:
20% de 120 =
120 * 1.2 =
144
Portanto, o aumento foi de R$24,00.
Valor subtraído da mensalidade da escola:
10% de 700 =
700 * 1.1 =
770
Portanto, o aumento foi de R$70,00.
Somando os valores 24 + 70, temos que o valor que precisa ser subtraído da mesada é de R$94,00.
Efetuando uma regra de três simples, temos que:
400 ------- 100
94 ------- x
400x = 100 * 94
400x = 9400
x = 9400/400
__________
|x = 23,5|
‾‾‾‾‾‾‾‾‾‾
2 - Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), o rendimento médio mensal dos trabalhadores brasileiros, no ano de 2000, era de R$1250,00. Já o censo de 2010 mostrou que esse valor teve um aumento de 7,2% em relação a 2000. Há uma projeção de que, em 2020, o rendimento médio mensal dos trabalhadores brasileiros será de 10% maior que em 2010. Supondo que as projeções estejam certas, o rendimento mensal dos brasileiros em 2020 será de:
a) R$1 340,00
b) R$1 349,00
c) R$1 375,00
d) R$1 465,00
e) R$1 474,00 <–
Salário de 2010:
Aumento de 7,2% em 1250 =
1250 * 1,072 =
1340
Salário em 2020:
Aumento de 10% em 1340 =
1340 * 1,1 =
______
|1474|
‾‾‾‾‾‾
3 - Um laboratório realiza exames em que é possível observar a taxa de glicose de uma pessoa. Os resultados são analisados de acordo com o quadro a seguir:
| glicemia | descrição |
|---|---|
| Hipoglicemia | taxa de glicose menor ou igual a 70mg/dL. |
| Normal | taxa de glicose maior que 70 mg/dL e menor ou igual a 100mg/dL. |
| Pré-diabetes | taxa de glicose maior que 100mg/dL e menor ou igual a 125mg/dL. |
| Diametes Melito | taxa de glicose maior que 125mg/dL e menor ou igual a 250mg/dL. |
| Hiperglicemia | taxa de glicose maior que 250mg/dL. |
Um paciente fez um exame de glicose nesse laboratório e comprovou que estava com hiperglicemia. Sua taxa de glicose era de 300mg/dL. Seu médico prescreveu um tratamento em duas etapas. Na primeira etapa ele conseguiu reduzir sua taxa em 30% e na segunda etapa em 10%.
Ao calcular sua taxa de glicose após as duas reduções, o paciente verificou que estava na categoria de:
a) hipoglicemia.
b) normal.
c) pré-diabetes.
d) diabetes melito. <–
e) hiperglicemia.
Redução de 30% em 300:
Pense que retirar 30% de um número é o mesmo que encontrar 70% dele mesmo, pois 100% - 30% = 70%.
70% de 300 =
300 * 0,7 =
210
Redução de 10% em 210:
O mesmo raciocínio se aplica ao 10%.
100% - 10% = 90%.
90% de 210 =
_____
|189|
‾‾‾‾‾
189 fica entre 125 e 250, portanto, se encaixa como diabetes melito.
Exercícios de Porcentagem e Revisão de Operações
08/03/2021
Exercícios de Porcentagem
Vimos nas duas últimas questões do formulário (as de resposta aberta) e corrigimos detalhadamente com discussões sobre as diferentes abordagens.
- Sara trabalha em uma loja de sapatos e ganha uma comissão de 25% sobre o valor das vendas que faz. Seu salário fixo é de 2000 reais. Qual valor ela deve vender em sapatos para que seu rendimento total seja 250% do seu salário fixo?
250% do salário = 250% de 2000
200% seria o dobro, logo 4000
50% seria a metade, logo 1000
Portanto 250% seria 5000
Se ela ganha 2000 e quer 5000, precisa ganhar mais 3000
Como 3000 com 25% de comissão é um quarto do total que ela precisa vender,
precisa vender (3000 * 4), logo 12000
- Júlio ganhou 50 reais de sua tia. Ela disse que ele tinha que dividir com a irmã dele e também guardar um pouco para uma eventual emergência. Júlio decidiu dar metade do valor para sua irmã e depois guardou 10 reais do que ficou com ele. A irmã disse que isso não seria justo e que ele deveria fazer o contrário, primeiro guardar 10 reais e depois dividir o que sobrou com ela pela metade. O que você acha dessa história? A ordem das operações faz mesmo diferença? Na sua opinião, o que Júlio deveria fazer? Porquê?
Nessa, existem diversas abordagens do que seria “justo”, vimos e discutimos acerca.
Revisão de operações
Demos uma pairada sobre conceitos “básicos” de ordem de operações, operações inversas, uso de parênteses para a mudança de ordem, e outros conceitos do gênero.
Operações
09/03/2021
Revimos mais sobre operações, com propriedades distributivas, forças das operações, mudanças dos resultados em função da ordem, etc.
Terminologia e Gráficos
05/04/2021
Exercícios de gráficos
06/04/2021
Revisamos o conceito de gráficos, servindo para mostrar comparações, tendências, etc.
Resolvemos o seguinte exercício juntos:
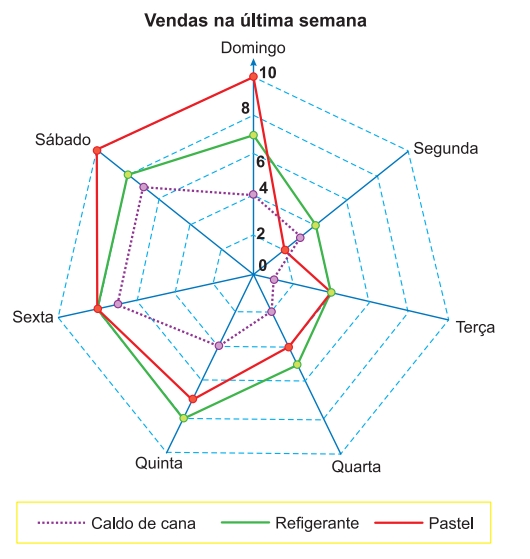
ENEM 2019: Um comerciante, que vende somente pastel, refrigerante em lata e caldo de cana em copos, fez um levantamento das vendas realizadas durante a semana. O resultado desse levantamento está apresentado no gráfico.
Ele estima que venderá, em cada dia da próxima semana, uma quantidade de refrigerante em lata igual à soma das quantidades de refrigerante em lata e caldo de cana em copos vendidas no respectivo dia da última semana.
Quanto aos pastéis, estima vender, a cada dia da próxima semana, uma quantidade igual à quantidade de refrigerante em lata que prevê vender em tal dia. Já para o número de caldo de cana em copos, estima que as vendas diárias serão iguais às da última semana.
Segundo essas estimativas, a quantidade a mais de pastéis que esse comerciante deve vender na próxima semana é:
a. 20.
b. 27.
c. 44.
d. 55.
e. 71.
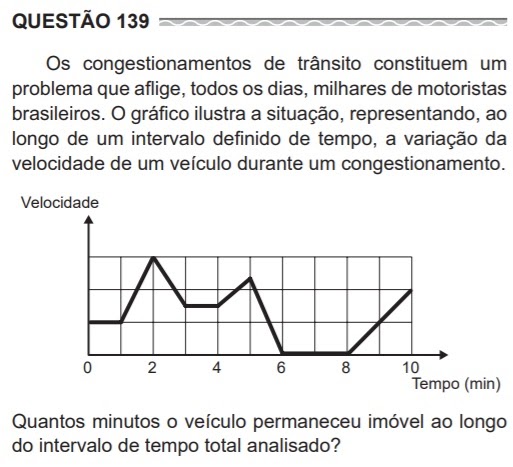
Também resolvemos juntos a seguinte questão:
a. 4.
b. 3.
c. 2.
d. 1.
e. 0.
Mais exercícios de análise de gráficos
07/04/2021
Finalização da retomada de Gráficos e Correção da ADE
12/04/2021
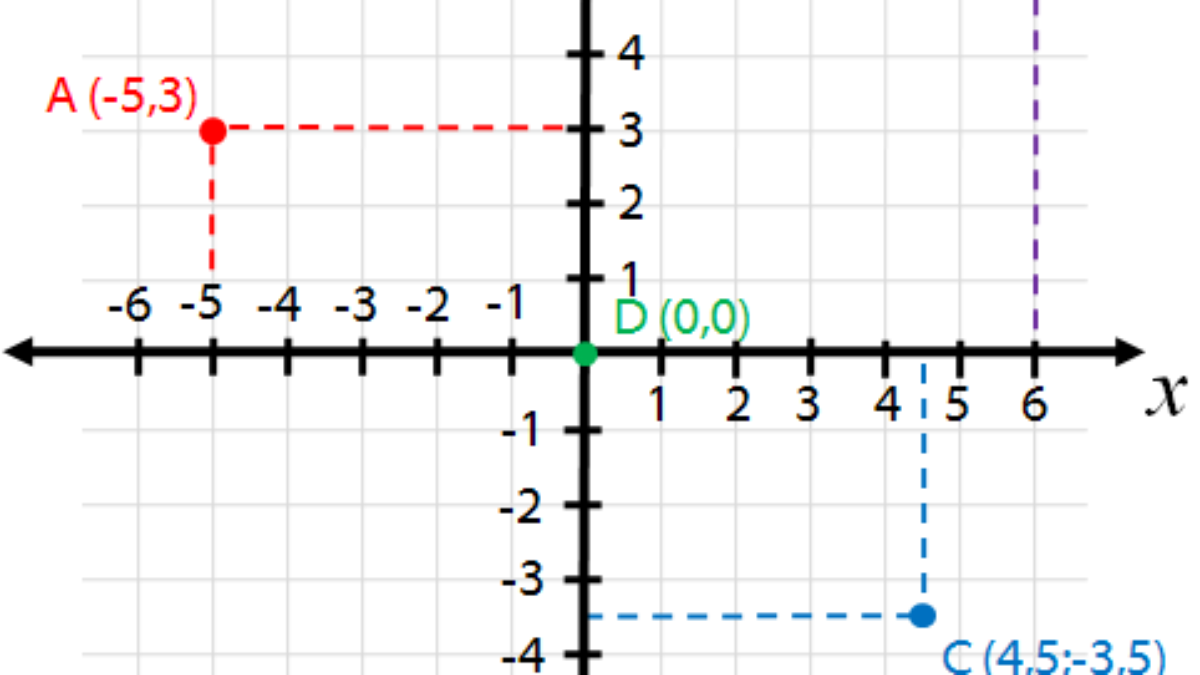
Vimos sobre Plano Cartesiano e a leitura de suas Coordenadas:
Correção da Avaliação Diagnóstica de Entrada (ADE):
Ex. 14:
Potências, raízes e conjuntos numéricos
13/04/2021
Potências quadradas
Qual é a área de um quadrado de lado 4?
Um quadrado de lado 4 é: 4 por 4.
Ou seja 4*4, ou 4^4 (4 elevado à 4).
4 vezes 4 é 16, então, a áre de um quadrado de lado 4 é 16.
Raiz quadrada
Na raiz quadrada a lógica é inversa, a pergunta é:
Qual é o lado do quadrado que tem 16 de área (ou 16 quadradinho dentro)?
Um quadrado com 16 dentro, tem de lado:
1 quadrado? - 1 vezes 1 é 1.
Não é 16.
2 quadrados? - 2 vezes 2 é 4.
Não é 16.
3 quadrados? - 3 vezes 3 é 9.
Não é 16.
4 quadrados? - 4 vezes 4 é 16.
É 16! Logo, um quadrado com 16 dentro, tem lado 4.
Conjuntos dos Numéricos Naturais
Números que usamos para fazer contagem.
Números inteiros, positivos.
N = { 0, 1, 2, 3, ..., 320, ..., 2021, ... }
Números naturais ao quadrado
0² = 0*0 = 0
1² = 1*1 = 1
2² = 2*2 = 4
3² = 3*3 = 9
...
Raíz quadrada
raiz de 0 = 0
raiz de 1 = 1
raiz de 4 = 2
raiz de 9 = 3
...
Conjunto dos Números Inteiros
Números positivos e negativos inteiros.
Z = { ..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ... }
Números inteiros ao quadrado
-3² = -3 * -3 = 9
-2² = -2 * -2 = 4
-1² = -1 * -1 = 1
0² = 0*0 = 0
1² = 1*1 = 1
2² = 2*2 = 4
3² = 3*3 = 9
...
Mas pera, tanto 2² quanto -2² dá 4.
Então a raiz de 4 pode ser -2 além de 2?
Sim, mas se fosse assim -2 seria igual a 2, o que é falso.
Por isso, foi feita uma convensão em que se decidiu ter a raiz de um número como sendo positiva.
raiz de 16 = 4
Porém, no caso de uma icógnita como:
x² = 16
4² = 16 é correto
-4² = 16 também é correto
Logo, x pode ser 4 ou -4
Conjuntos dos Numéricos Racionais
Números que vêm de uma divisão.
Se temos:
C = A / B
Sendo A e B inteiros e diferentes de 0.
Temos que:
C pertence aos números racionais.
15/5 = 3
3 é racional
e inteiro
-3/10 = -0,3
-0,3 é racional
e decimal exato
1/3 = 0,333...
0,333... é racional
e dízima periódica
Teorema de Pitágoras
19/04/2021
Lados do Triângulo Retângulo
Os lados que formam o ânculo reto, se chamam-se catetos.
O terceiro lado, maior, oposto ao ângulo reto, é a hipotenusa.
Teorema de Pitágoras
“O quadrado da hipotenusa é igual a soma dos quadrados dos catetos”
Para visualizar, vimos o seguinte vídeo: A demonstração do Teorema de Pitágoras(via experimento) - YouTube

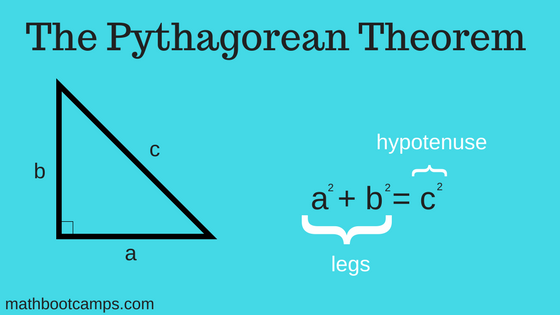
Qual é a medida do lado a?
Temos vários triângulo reângulos retos:
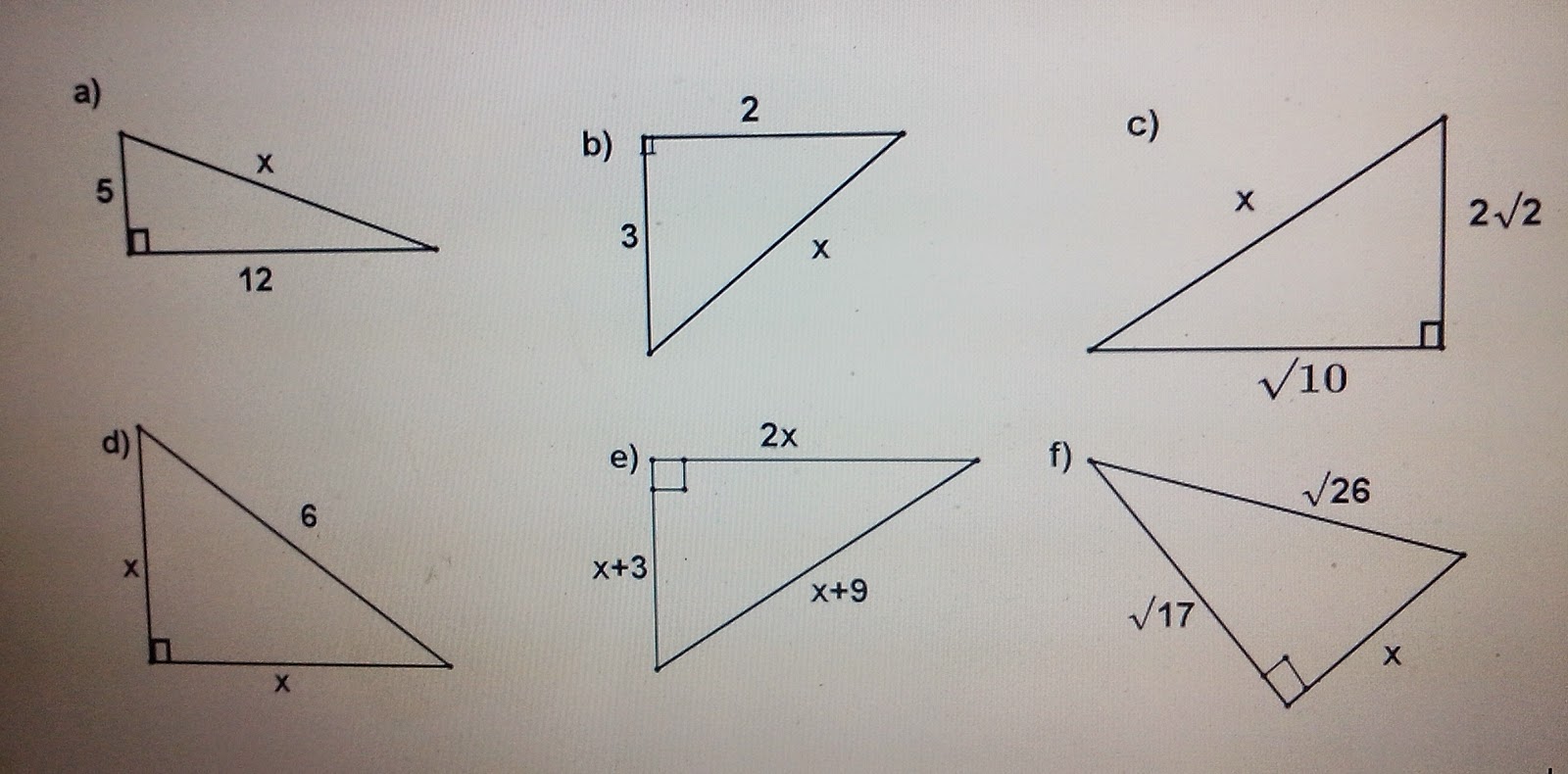
Na fórmula, a e b são catetos, c é a hipotenusa. Se consideraros o triângulo b:
c² = a² + b²
c² = 2² + 3²
c³ = 4 + 9
c² = 13
c = raíz de 13
Conjunto dos números Reais
Os números reais englobam todos os outros conjuntos que vimos até agora.
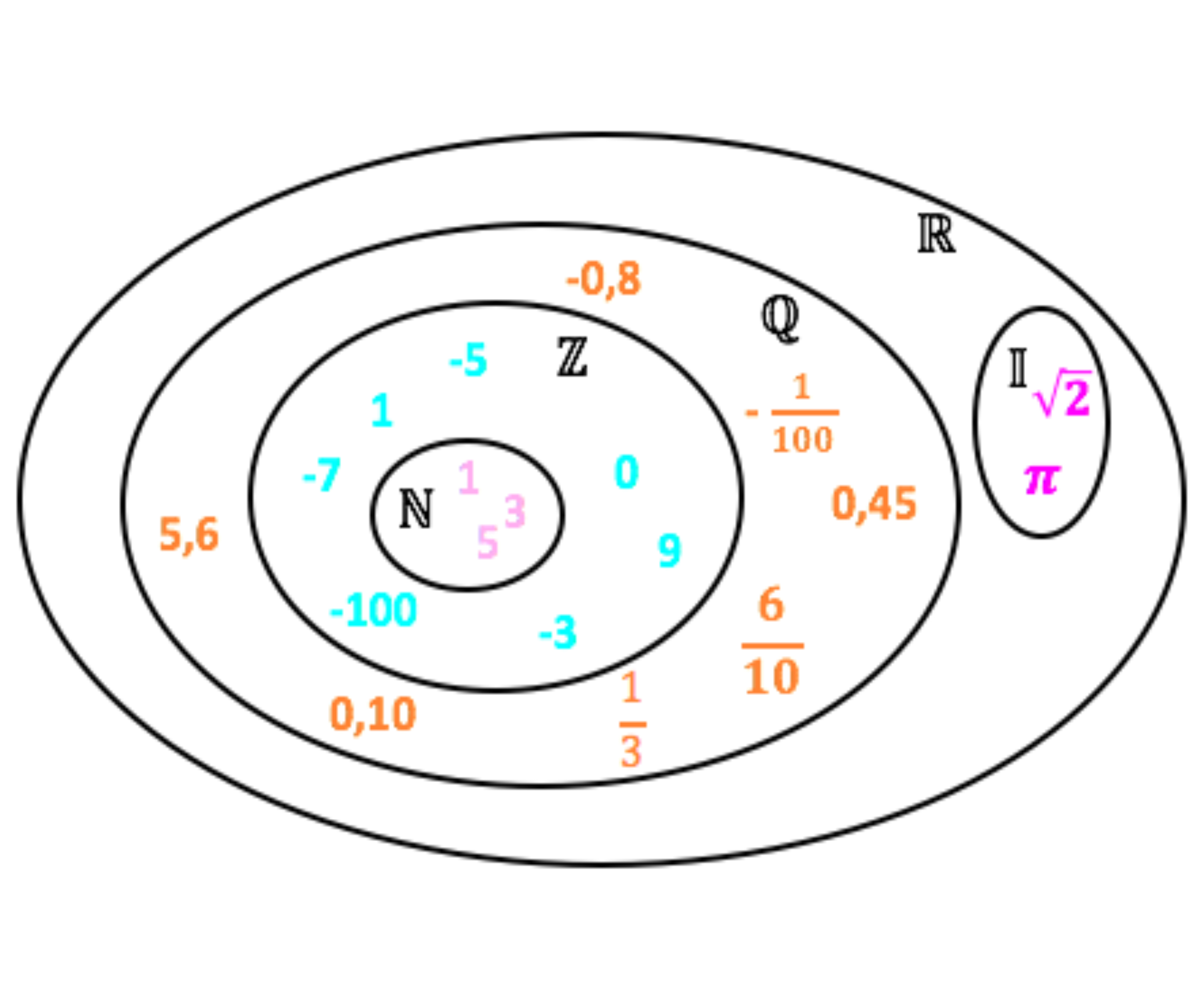
ℝ é o símbolo dos números racionais.
Números Reais
20/04/2021
Operações com Números Reais
10/05/2021
Razões Trigonométricas
11/05/2021